Materi matematika polinomial membahas tentang fungsi polinomial, mulai dari definisi dan jenis-jenisnya hingga operasi, faktorisasi, persamaan, grafik, dan aplikasinya dalam kehidupan sehari-hari. Dari yang sederhana hingga yang kompleks, materi ini akan mengupas tuntas setiap aspek polinomial, memberikan pemahaman yang komprehensif dan aplikatif.
Kita akan memulai dengan memahami konsep dasar polinomial, seperti definisi, jenis berdasarkan derajat, dan hubungannya dengan bentuk grafik. Selanjutnya, kita akan mempelajari berbagai operasi pada polinomial, mulai dari penjumlahan, pengurangan, perkalian, dan pembagian. Tidak hanya itu, kita juga akan mendalami faktorisasi polinomial, menyelesaikan persamaan polinomial, memahami grafiknya, dan melihat bagaimana konsep ini diterapkan dalam berbagai bidang seperti fisika, teknik, dan ekonomi.
Definisi dan Konsep Dasar Polinomial
Polinomial merupakan ekspresi aljabar yang terdiri dari variabel, koefisien, dan konstanta. Polinomial memiliki berbagai derajat dan bentuk grafik yang berbeda, tergantung pada derajatnya. Pemahaman tentang polinomial sangat penting dalam berbagai bidang matematika dan aplikasinya.
Definisi Matematis Polinomial
Secara matematis, polinomial adalah ekspresi yang terdiri dari variabel dan koefisien, di mana variabelnya hanya berpangkat bilangan bulat non-negatif. Operasi yang diizinkan meliputi penjumlahan, pengurangan, perkalian, dan pemangkatan variabel dengan bilangan bulat non-negatif.
Contoh: 3x2 + 2x – 1
Jenis-Jenis Polinomial Berdasarkan Derajatnya
Polinomial diklasifikasikan berdasarkan derajat tertinggi dari variabelnya. Derajat polinomial menunjukkan seberapa kompleks polinomial tersebut. Berikut beberapa jenisnya:
- Polinomial Konstan: Polinomial dengan derajat nol, contohnya: 5
- Polinomial Linear: Polinomial dengan derajat satu, contohnya: 2x + 3
- Polinomial Kuadrat: Polinomial dengan derajat dua, contohnya: x 2
-4x + 4 - Polinomial Kubik: Polinomial dengan derajat tiga, contohnya: x 3 + 2x 2
-5x + 1 - Polinomial Tertinggi: Polinomial dengan derajat empat atau lebih.
Contoh Polinomial dengan Derajat Berbeda
Berikut beberapa contoh polinomial dengan derajat yang berbeda:
- Derajat 0: 7
- Derajat 1: 2x – 5
- Derajat 2: x 2 + 3x + 2
- Derajat 3: x 3
-6x 2 + 11x – 6 - Derajat 4: 2x 4 + x 3
-5x 2 + 3x – 1
Hubungan Derajat dan Bentuk Grafik Polinomial
Bentuk grafik polinomial dipengaruhi oleh derajatnya. Grafik polinomial dengan derajat yang berbeda memiliki bentuk yang berbeda pula.
| Derajat | Bentuk Grafik | Contoh |
|---|---|---|
| 0 | Garis horizontal | y = 5 |
| 1 | Garis lurus | y = 2x + 3 |
| 2 | Parabola | y = x2 – 4x + 4 |
| 3 | Kurva dengan satu titik balik maksimum/minimum | y = x3 + 2x2 – 5x + 1 |
| 4 atau lebih | Kurva dengan lebih dari satu titik balik maksimum/minimum | y = 2x4 + x3
|
Perubahan Grafik Polinomial Seiring Perubahan Derajat
Semakin tinggi derajat polinomial, semakin kompleks bentuk grafiknya. Grafik dapat memiliki lebih banyak titik balik, dan perubahan arahnya lebih banyak. Polinomial dengan derajat tinggi dapat memiliki banyak titik potong dengan sumbu x.
Operasi pada Polinomial: Materi Matematika Polinomial
Operasi pada polinomial melibatkan penjumlahan, pengurangan, perkalian, dan pembagian. Pemahaman tentang operasi-operasi ini sangat penting untuk berbagai aplikasi matematika, khususnya dalam penyelesaian persamaan dan analisis fungsi.
Penjumlahan dan Pengurangan Polinomial
Penjumlahan dan pengurangan polinomial dilakukan dengan menggabungkan suku-suku sejenis. Suku sejenis adalah suku-suku yang memiliki variabel dan pangkat yang sama.
- Untuk menjumlahkan polinomial, tambahkan koefisien dari suku-suku sejenis.
- Untuk mengurangkan polinomial, kurangi koefisien dari suku-suku sejenis.
Contoh Soal dan Penyelesaian
Misalkan polinomial P(x) = 3x 2 + 2x – 5 dan Q(x) = x 2
-4x + 2.
- Penjumlahan: P(x) + Q(x) = (3x 2 + 2x – 5) + (x 2
- 4x + 2) = 4x 2
- 2x – 3
- Pengurangan: P(x)
- Q(x) = (3x 2 + 2x – 5)
- (x 2
- 4x + 2) = 2x 2 + 6x – 7
Perkalian Polinomial, Materi matematika polinomial
Perkalian polinomial melibatkan mengalikan setiap suku dalam satu polinomial dengan setiap suku dalam polinomial lainnya, kemudian menggabungkan suku-suku sejenis.
- Metode distributif dapat digunakan untuk mengalikan polinomial.
Contoh Soal dan Penyelesaian
Misalkan polinomial P(x) = 2x + 3 dan Q(x) = x – 1.
- P(x)
- Q(x) = (2x + 3)(x – 1) = 2x2
- 2x + 3x – 3 = 2x 2 + x – 3
Pembagian Polinomial
Pembagian polinomial dapat dilakukan dengan metode Horner atau metode lain yang relevan, tergantung pada bentuk polinomial yang dibagi.
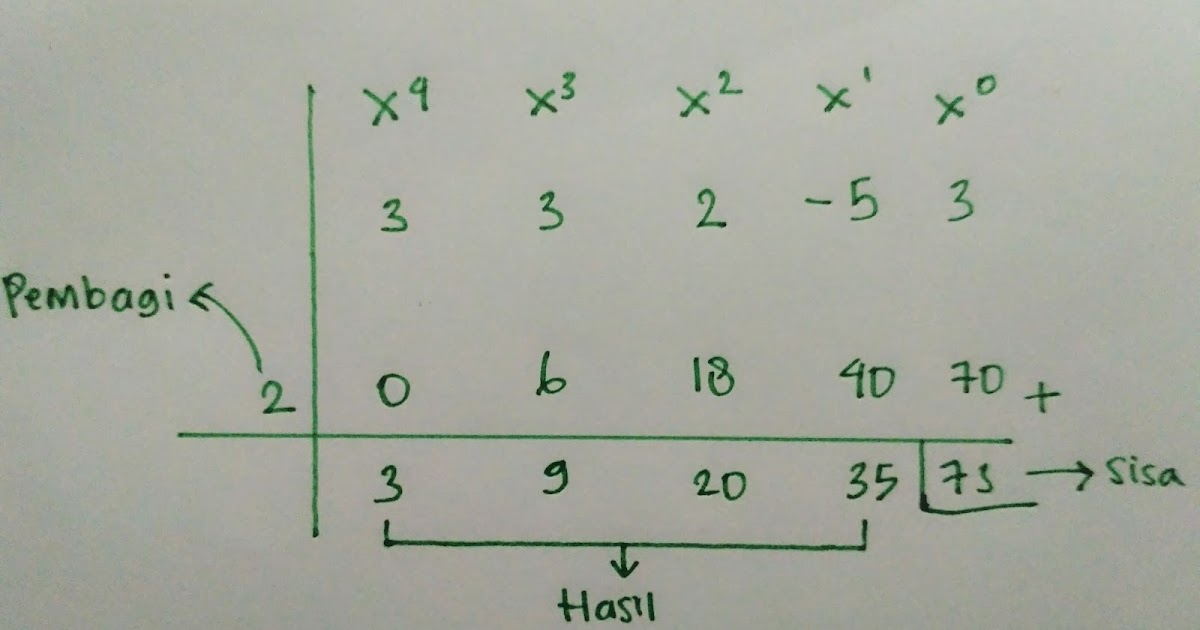
Metode Horner
Metode Horner digunakan untuk membagi polinomial dengan faktor linear. Metode ini efisien untuk pembagian polinomial derajat tinggi.
Contoh Soal dan Penyelesaian
Misalkan polinomial P(x) = 2x 3 + 5x 2
-4x + 3 dan kita ingin membagi dengan (x – 2).
| Langkah | Deskripsi |
|---|---|
| 1 | Tulis koefisien polinomial P(x) dalam urutan menurun. |
| 2 | Tulis nilai yang membuat pembagi menjadi nol (x – 2 = 0, maka x = 2). |
| 3 | Turunkan koefisien pertama (2) ke baris bawah. |
| 4 | Kalikan nilai yang membuat pembagi menjadi nol (2) dengan koefisien yang diturunkan (2), tulis hasilnya di kolom berikutnya. (2 x 2 = 4) |
| 5 | Jumlahkan koefisien (5 + 4 = 9) |
| 6 | Ulangi langkah 4 dan 5 hingga semua koefisien diproses. |
Hasil pembagian dengan metode Horner adalah 2x 2 + 9x + 14 dengan sisa 31.
Faktorisasi Polinomial

Faktorisasi polinomial merupakan proses penting dalam aljabar, yang memungkinkan kita untuk memecah polinomial menjadi faktor-faktor yang lebih sederhana. Pemahaman tentang teknik faktorisasi ini sangat berguna dalam menyelesaikan persamaan polinomial dan berbagai aplikasi matematika lainnya.
Teknik Faktorisasi Polinomial
Berbagai teknik faktorisasi polinomial dapat digunakan, tergantung pada bentuk polinomial yang dihadapi. Berikut beberapa teknik umum yang sering digunakan:
- Faktorisasi dengan pemfaktoran umum: Jika terdapat faktor yang sama pada semua suku dalam polinomial, faktor tersebut dapat difaktorkan keluar. Misalnya, dalam polinomial 3x 2 + 6x, faktor 3x dapat difaktorkan keluar, menghasilkan 3x(x + 2).
- Faktorisasi dengan menggunakan selisih kuadrat: Teknik ini berlaku untuk polinomial yang mengikuti pola a 2
-b 2, yang dapat difaktorkan menjadi (a – b)(a + b). Contohnya, x 2
-9 dapat difaktorkan menjadi (x – 3)(x + 3). - Faktorisasi dengan menggunakan metode pengelompokan: Metode ini berguna untuk polinomial dengan empat atau lebih suku. Suku-suku dikelompokkan sedemikian rupa sehingga faktor-faktor yang sama dapat difaktorkan keluar dari masing-masing kelompok.
- Faktorisasi dengan menggunakan rumus perkalian istimewa: Beberapa rumus perkalian istimewa dapat mempercepat proses faktorisasi. Contohnya, (a + b) 2 = a 2 + 2ab + b 2 atau (a – b) 2 = a 2
-2ab + b 2.
Penerapan Faktorisasi dalam Menyelesaikan Persamaan Polinomial
Faktorisasi sangat penting dalam menyelesaikan persamaan polinomial. Jika sebuah polinomial dapat difaktorkan menjadi bentuk (x – a)(x – b)(x – c) = 0, maka akar-akar persamaan polinomial tersebut adalah a, b, dan c. Dengan mengetahui akar-akarnya, kita dapat menentukan nilai-nilai x yang memenuhi persamaan tersebut.
Contoh Soal dan Penyelesaian
Berikut contoh faktorisasi polinomial dengan faktor-faktor yang berbeda:
- Contoh 1: Faktorkan polinomial x 25x + 6. Polinomial ini dapat difaktorkan menjadi (x – 2)(x – 3).
- Contoh 2: Faktorkan polinomial 2x 2 + 4x. Dengan pemfaktoran umum, faktor 2x dapat difaktorkan keluar, menghasilkan 2x(x + 2).
Diagram Alir Penentuan Metode Faktorisasi
Untuk menentukan metode faktorisasi yang tepat, berikut diagram alir sederhana:
| Langkah | Kondisi | Metode |
|---|---|---|
| 1 | Jumlah suku dalam polinomial | Pilih metode yang sesuai dengan jumlah suku, seperti pemfaktoran umum atau pengelompokan. |
| 2 | Bentuk polinomial | Periksa apakah polinomial tersebut mengikuti pola selisih kuadrat atau rumus perkalian istimewa. |
| 3 | Keberadaan faktor umum | Jika ada faktor umum, faktorkan keluar faktor tersebut. |
Faktorisasi dengan Menggunakan Akar-Akar
Teknik ini melibatkan penggunaan akar-akar polinomial untuk menentukan faktor-faktornya. Jika akar-akar diketahui, kita dapat membangun faktor-faktornya. Misalnya, jika akar-akar suatu polinomial adalah 2 dan 3, maka faktor-faktornya adalah (x – 2) dan (x – 3).
Persamaan Polinomial
Persamaan polinomial merupakan persamaan yang melibatkan variabel dan koefisien dalam bentuk polinomial. Pemecahan persamaan polinomial derajat tinggi memerlukan teknik khusus, seperti teorema akar-akar rasional dan metode numerik. Memahami cara menyelesaikan persamaan polinomial ini sangat penting dalam berbagai aplikasi, dari perhitungan fisika hingga rekayasa.
Menyelesaikan Persamaan Polinomial Derajat Tertentu
Untuk menyelesaikan persamaan polinomial derajat tertentu, pendekatan yang tepat tergantung pada derajat polinomial. Untuk derajat rendah (misalnya, derajat 2, 3), metode aljabar seperti rumus kuadrat, rumus kubik, atau metode faktorisasi dapat digunakan. Untuk derajat yang lebih tinggi, metode numerik seperti metode Newton-Raphson atau metode iterasi dapat membantu menemukan akar-akar perkiraan.
Teorema Akar-Akar Rasional dan Penerapannya
Teorema akar-akar rasional memberikan kriteria untuk menemukan akar-akar rasional dari persamaan polinomial dengan koefisien integer. Teorema ini sangat membantu dalam menyederhanakan proses pencarian akar, karena kita hanya perlu memeriksa pembagi dari konstanta suku tetap dibagi oleh pembagi dari koefisien suku tertinggi. Dengan demikian, kita dapat membatasi kemungkinan akar rasional yang ada.
- Teorema ini menyatakan bahwa jika suatu persamaan polinomial dengan koefisien integer memiliki akar rasional, maka akar tersebut harus berupa pecahan yang pembilangnya merupakan faktor dari konstanta suku tetap dan penyebutnya merupakan faktor dari koefisien suku tertinggi.
- Penerapan teorema ini mempercepat proses pencarian akar-akar rasional, sehingga mempermudah penyelesaian persamaan polinomial.
Contoh Soal dan Penyelesaian Persamaan Polinomial dengan Akar Kompleks
Contoh soal persamaan polinomial dengan akar kompleks dapat melibatkan polinomial derajat tinggi yang memiliki akar-akar kompleks konjugat. Menentukan akar-akar kompleks memerlukan pemahaman tentang sifat-sifat akar kompleks konjugat dan mungkin melibatkan penggunaan rumus-rumus khusus untuk menyelesaikannya.
Misalnya: Tentukan akar-akar dari x3
3x2 + 4x – 2 = 0.
Setelah diaplikasikan teorema akar-akar rasional dan metode lainnya, kita mungkin menemukan akar real dan kompleks. Prosesnya mungkin melibatkan faktorisasi polinomial atau penggunaan rumus khusus untuk menyelesaikannya.
Penerapan dalam Pemecahan Masalah Dunia Nyata
Persamaan polinomial memiliki aplikasi luas dalam berbagai bidang, seperti fisika, teknik, dan ekonomi. Contohnya, dalam fisika, persamaan polinomial dapat digunakan untuk memodelkan lintasan suatu benda yang dilempar. Dalam teknik, persamaan polinomial dapat digunakan untuk menentukan dimensi struktur yang stabil.
- Dalam model pertumbuhan populasi, persamaan polinomial dapat digunakan untuk memodelkan pertumbuhan populasi selama beberapa periode waktu.
- Dalam rekayasa, persamaan polinomial dapat digunakan untuk memodelkan perilaku sistem mekanik.
Menentukan Akar-Akar Rasional dan Kompleks dengan Berbagai Teknik
Teknik yang digunakan untuk menentukan akar-akar rasional dan kompleks dapat bervariasi tergantung pada karakteristik polinomial. Selain teorema akar-akar rasional, metode lainnya seperti pembagian panjang polinomial, metode faktorisasi, dan metode numerik (seperti metode Newton-Raphson) dapat digunakan untuk menyelesaikan persamaan polinomial.
| Teknik | Deskripsi |
|---|---|
| Pembagian Panjang Polinomial | Membagi polinomial dengan faktor yang diketahui untuk mencari faktor-faktor lain. |
| Metode Faktorisasi | Memfaktorkan polinomial menjadi faktor-faktor linier atau kuadrat. |
| Metode Numerik (Newton-Raphson) | Mencari akar perkiraan dengan iterasi. |
Grafik Polinomial
Grafik polinomial memberikan gambaran visual tentang perilaku fungsi polinomial. Memahami bentuk dan ciri-ciri grafik sangat penting untuk menganalisis dan menyelesaikan masalah yang melibatkan polinomial.
Penggambaran Grafik Berdasarkan Koefisien dan Derajat
Bentuk grafik polinomial sangat dipengaruhi oleh derajat dan koefisien utama. Derajat menentukan jumlah maksimum titik belok dan jumlah maksimum akar real. Koefisien utama menentukan arah kecenderungan grafik untuk nilai x yang sangat besar.
- Grafik polinomial berderajat ganjil selalu memiliki kecenderungan yang berlawanan pada ujung-ujungnya. Jika koefisien utama positif, grafik naik ke tak hingga untuk x yang besar dan turun ke tak hingga untuk x yang kecil. Sebaliknya, jika koefisien utama negatif, grafik turun ke tak hingga untuk x yang besar dan naik ke tak hingga untuk x yang kecil.
- Grafik polinomial berderajat genap selalu memiliki kecenderungan yang sama pada ujung-ujungnya. Jika koefisien utama positif, grafik naik ke tak hingga untuk x yang sangat besar dan kecil. Sebaliknya, jika koefisien utama negatif, grafik turun ke tak hingga untuk x yang sangat besar dan kecil.
Penentuan Titik Potong Sumbu x dan y
Titik potong sumbu x merupakan akar-akar dari persamaan polinomial, yang dapat dihitung dengan metode faktorisasi atau rumus-rumus yang sesuai. Titik potong sumbu y terjadi saat x = 0, sehingga nilai y langsung diperoleh dengan mensubstitusikan x = 0 ke dalam persamaan polinomial.
Ilustrasi Grafik Polinomial
Grafik polinomial x 3
-3x 2
-6x + 8 akan memiliki titik potong sumbu x pada x = -1, x = 2, dan x = 4. Titik potong sumbu y terjadi saat x = 0, sehingga y = 8. Grafik akan naik ke tak hingga untuk nilai x yang besar dan turun ke tak hingga untuk nilai x yang kecil karena koefisien utama positif dan derajat ganjil.
Grafik ini akan memiliki dua titik belok.
Perilaku Grafik Berdasarkan Koefisien dan Derajat
Perilaku grafik polinomial dapat diprediksi berdasarkan derajat dan tanda koefisien utama. Semakin tinggi derajat, semakin kompleks bentuk grafiknya. Tanda koefisien utama menentukan arah kecenderungan grafik untuk nilai x yang sangat besar. Misalnya, polinomial dengan derajat 5 dan koefisien utama positif akan naik ke tak hingga untuk nilai x yang besar dan turun ke tak hingga untuk nilai x yang kecil.
Sifat-Sifat Grafik Polinomial dan Penafsirannya
Grafik polinomial memiliki sifat-sifat yang dapat ditafsirkan. Misalnya, titik belok menunjukkan perubahan arah grafik. Grafik polinomial derajat n memiliki paling banyak n-1 titik belok. Interpretasi terhadap grafik dapat membantu dalam memahami solusi dari persamaan atau pertidaksamaan yang melibatkan polinomial tersebut.
Aplikasi Polinomial dalam Kehidupan Sehari-hari
Polinomial, sebagai fungsi matematika yang sederhana namun powerful, memiliki berbagai aplikasi di berbagai bidang kehidupan. Dari perhitungan fisika hingga perancangan kurva ekonomi, polinomial menunjukkan fleksibilitasnya dalam memodelkan berbagai fenomena.
Penerapan Polinomial dalam Fisika
Dalam fisika, polinomial sering digunakan untuk memodelkan gerak benda. Misalnya, persamaan gerak parabola, yang menggambarkan lintasan proyektil, dapat dinyatakan dalam bentuk polinomial. Kecepatan dan posisi benda pada berbagai waktu dapat dihitung dengan persamaan polinomial derajat tertentu. Hal ini memungkinkan para ilmuwan dan insinyur untuk memprediksi perilaku benda yang dilempar atau bergerak di bawah pengaruh gravitasi.
Penerapan Polinomial dalam Teknik
Di bidang teknik sipil, polinomial digunakan untuk memodelkan beban struktur dan menghitung tegangan. Dalam teknik mesin, polinomial dapat digunakan untuk memodelkan kecepatan dan percepatan mesin. Misalnya, polinomial dapat digunakan untuk menghitung beban pada jembatan berdasarkan model distribusi beban yang kompleks. Dengan memahami polinomial, insinyur dapat merancang struktur yang lebih kuat dan efisien.
Penerapan Polinomial dalam Ekonomi
Dalam ekonomi, polinomial dapat digunakan untuk memodelkan pertumbuhan dan penurunan populasi, permintaan, dan penawaran suatu produk. Contohnya, model pertumbuhan populasi dapat menggunakan polinomial untuk memperkirakan jumlah populasi pada waktu tertentu. Hal ini memungkinkan para ekonom untuk memprediksi tren ekonomi dan membuat perencanaan yang lebih baik.
Model Matematika dengan Polinomial
Banyak fenomena alam dapat dijelaskan dengan model matematika yang menggunakan polinomial. Model-model ini memberikan gambaran yang akurat tentang bagaimana suatu fenomena berubah seiring waktu atau terhadap variabel lainnya. Sebagai contoh, pertumbuhan bakteri pada suatu medium dapat dimodelkan dengan persamaan polinomial yang memperhitungkan faktor-faktor seperti nutrisi dan temperatur. Model ini penting untuk memahami dan memprediksi pertumbuhan bakteri dalam berbagai kondisi.
Contoh Penerapan dalam Pertumbuhan Populasi
Pertumbuhan populasi seringkali dapat didekati dengan model polinomial. Bayangkan populasi hewan tertentu yang awalnya kecil, tetapi kemudian mengalami pertumbuhan eksponensial. Dengan mengukur populasi pada beberapa waktu tertentu, kita dapat menentukan persamaan polinomial yang mendekati pertumbuhan tersebut. Contohnya, pada tahun ke-0 populasi hewan tersebut berjumlah 100, tahun ke-1 berjumlah 120, dan tahun ke-2 berjumlah 144. Dari data ini, kita dapat membuat persamaan polinomial untuk memprediksi populasi pada tahun-tahun berikutnya.
Perancangan Kurva dengan Polinomial
Polinomial sangat berguna dalam perancangan kurva. Bentuk kurva yang kompleks dapat didekati dengan polinomial. Sebagai ilustrasi, bayangkan Anda ingin merancang sebuah jalur kereta api yang melintasi bukit. Untuk membuat jalur yang mulus dan aman, Anda dapat menggunakan polinomial untuk memodelkan bentuk bukit dan merancang jalur yang sesuai. Ini memungkinkan insinyur sipil untuk merancang struktur yang lebih aman dan lebih efisien.
Ilustrasi Grafik Penerapan Polinomial
Grafik polinomial dapat menggambarkan hubungan antara variabel-variabel dalam suatu model. Sebagai contoh, grafik dapat memperlihatkan hubungan antara waktu dan jumlah populasi hewan. Grafik tersebut dapat menunjukkan bagaimana populasi hewan tersebut meningkat atau menurun seiring waktu. Bentuk grafik ini akan bervariasi tergantung pada persamaan polinomial yang digunakan untuk memodelkan fenomena tersebut.
Kesimpulan
Melalui pembahasan komprehensif ini, diharapkan pembaca dapat memahami secara mendalam materi matematika polinomial. Pemahaman yang utuh tentang konsep, operasi, dan aplikasi polinomial akan memperkuat kemampuan analitis dan pemecahan masalah. Semoga materi ini dapat menjadi dasar yang kuat untuk mempelajari konsep-konsep matematika yang lebih lanjut.